 MONTGOMERY COUNTY PUBLIC SCHOOLS
MONTGOMERY COUNTY PUBLIC SCHOOLS
 MONTGOMERY COUNTY PUBLIC SCHOOLS
MONTGOMERY COUNTY PUBLIC SCHOOLS
If you weighed four objects in pounds, then weighed the same four objects in kilograms, you might come up with this table.
| weight (pounds) | weight (kilograms) |
|---|---|
| 22 | 10 |
| 88 | 40 |
| 33 | 15 |
| 40.7 | 18.5 |
Students are using what they know about ratios and rates to reason about measurements in different units of measurement such as pounds and kilograms. In earlier grades, students converted yards to feet using the fact that 1 yard is 3 feet, and kilometers to meters using the fact that 1 kilometer is 1,000 meters. Now in grade 6, students convert units that do not always use whole numbers.
Here is a task to try with your student:
Explain your strategy for each question.
Solution:
Any correct strategy that your student understands and can explain is acceptable. Sample strategies:
Who biked faster: Andre, who biked 25 miles in 2 hours, or Lin, who biked 30 miles in 3 hours? One strategy would be to calculate a unit rate for each person. A unit rate is an equivalent ratio expressed as something “per 1.” For example, Andre’s rate could be written as “
Every ratio has two unit rates. In this example, we could also compute hours per mile: how many hours it took each person to cover 1 mile. Although not every rate has a special name, rates in “miles per hour” are commonly called speed and rates in “hours per mile” are commonly called pace.
Andre:
| distance (miles) | time (hours) |
|---|---|
| 25 | 2 |
| 1 | 0.08 |
| 12.5 | 1 |
Lin:
| distance (miles) | time (hours) |
|---|---|
| 30 | 3 |
| 10 | 1 |
| 1 | 0.1 |
Here is a task to try with your student:
Dry dog food is sold in bulk: 4 pounds for $16.00.
Solution:
| dog food (pounds) | cost (dollars) |
|---|---|
| 4 | 16 |
| 1 | 4 |
| 0.25 | 1 |
Let’s say 440 people attended a school fundraiser last year. If 330 people were adults, what percentage of people were adults? If it’s expected that the attendance this year will be 125% of last year, how many attendees are expected this year? A double number line can be used to reason about these questions.
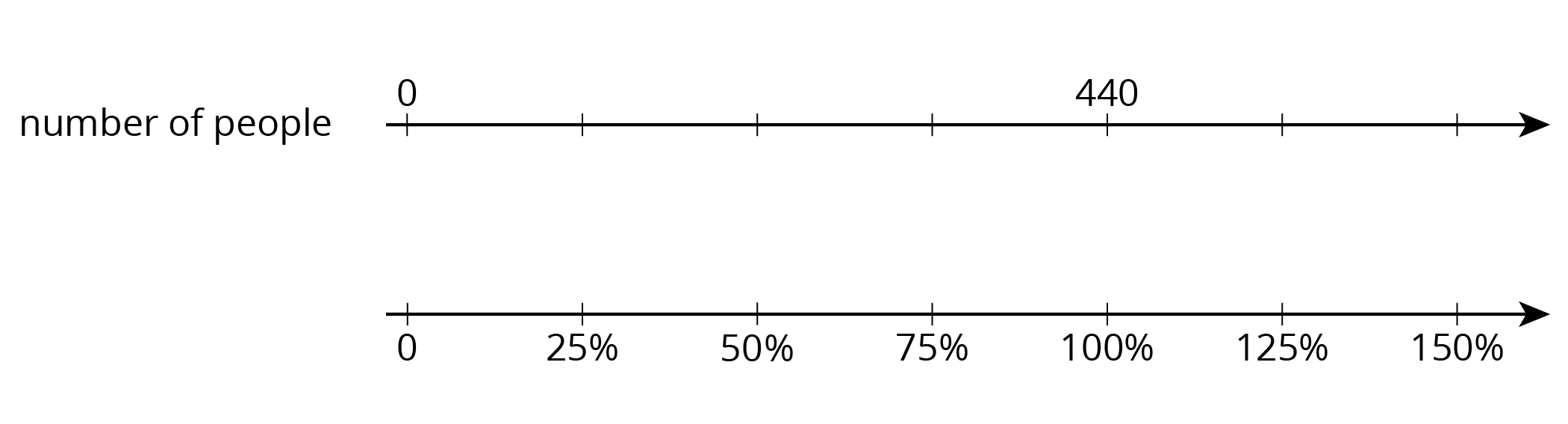
Students use their understanding of “rates per 1” to find percentages, which we can think of as “rates per 100.” Double number lines and tables continue to support their thinking. The example about attendees of a fundraiser could also be organized in a table:
| number of people | percentage |
|---|---|
| 440 | 100% |
| 110 | 25% |
| 330 | 75% |
| 550 | 125% |
Toward the end of the unit, students develop more sophisticated strategies for finding percentages. For example, you can find 125% of 440 attendees by computing
Here is a task to try with your student:
For each question, explain your reasoning. If you get stuck, try creating a table or double number line for the situation.
Solution:
Any correct reasoning that a student understands and can explain is acceptable. Sample reasoning:
IM 6–8 Math was originally developed by Open Up Resources and authored by Illustrative Mathematics, and is copyright 2017-2019 by Open Up Resources. It is licensed under the Creative Commons Attribution 4.0 International License (CC BY 4.0). OUR's 6–8 Math Curriculum is available at https://openupresources.org/math-curriculum/.