Mathematics Support

Videos

• Video 1: Building a Model (Lessons 1–3)
• Video 2: Solutions to Linear Equations (Lessons 4–6)
• Video 3: Rewriting Equations (Lessons 7–9)
• Video 4: Equations and Their Graphs (Lessons 10–12)
• Video 5: Solving Systems of Equations (Lessons 13–17)
• Video 6: One-Variable Inequalities (Lessons 18–20)
• Video 7: Systems of Inequalities (Lessons 21–25)

In this unit, your student will analyze constraints on different quantities. For example, the amount you spend on groceries may be limited by your budget. To qualify for a sports team, you may need to practice at least a certain number of hours, or lift at least a certain number of pounds. Here are some ways to write constraints using mathematical notation: w<20. An apartment building only allows dogs that weigh less than 20 pounds. m+g+b=4. A casserole recipe calls for four cups of vegetables. You have mushrooms, green beans, and broccoli. 12.5c+15a=1,000. In order for a concert to be performed, the artists need to be sure of 1,000 in ticket sales. Tickets for children under 18 are 12.50 and tickets for adults are 15.5n + 10d = 150. You need 1.50 in coins for a parking meter. You have a bunch of nickels and dimes in your pocket. For this last situation, we can see that using more dimes to make $1.50 means that we can use fewer nickels, and vice-versa. A graph allows us to see this relationship even more clearly.

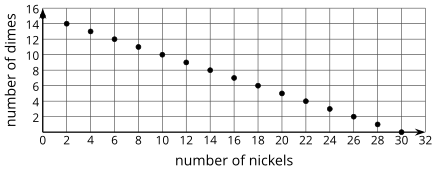
 Each point on the graph represents a combination of nickels and dimes that totals $1.50. For example, if you use 8 nickels, you will need 11 dimes.

Here is a task to try with your student:

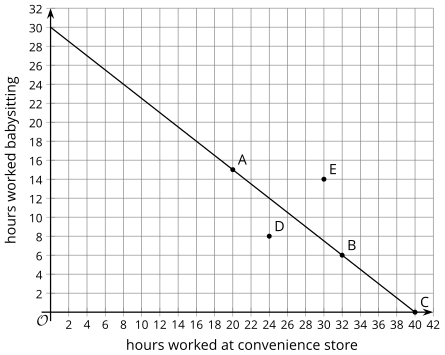
Priya is saving money to go on an overnight school trip. The cost of the trip is 360. She has a job at a convenience store, which pays 9 per hour, and sometimes babysits for a family in her neighborhood, which pays 12 per hour. The equation 9x + 12y = 360 represents all the combinations of hours Priya could work at each job and earn a total of 360. Here is a graph showing those combinations.

1. What are the coordinates of point A?
2. What does it tell us about the number of hours Priya worked at each job?
3. Answer the same questions about points B and C.
4. Point D is not on the line. How should we interpret point D?
5. Point E is not on the line. How should we interpret point E?

Solution

1. (20,15)
2. Priya works 20 hours at the convenience store and 15 hours babysitting.
3. Point B: (36,6). Priya works 32 hours at the convenience store and 6 hours babysitting. Point C: (40,0). Priya works 40 hours at the convenience store and does not babysit at all.
4. Priya does not make enough money. She works 24 hours at the convenience store and 8 hours babysitting. She makes only $312, since 24·9+8·12=312.
5. Priya makes more than enough money: $438. She works 30 hours at the convenience store and 14 hours babysitting. 30·9+14·12=438.